Performansi panel surya dapat diselidiki dengan dilakukannya simulasi menggunakan komputer, untuk keperluan ini maka rangkaian ekivalen seperti pada gambar III.7 dan permodelannnya secara secara matematis sangatlah diperlukan. Permodelan yang diterapkan dalam penelitian merujuk pada referensi [30]. Besar arus I yang dihasilkan proporsional dengan persamaan III.5.
dimana,
:Arus saturasi dioda
|
|
:Konstanta dioda. 1≤ a ≤2
|
|
IPV
|
:Light-generated current (A)
|
RS
|
:Resistansi seri
|
RP
|
:Resistansi paralel
|
Vt
|
:Resistansi termis
|
NS
|
:Jumlah sel terpasang seri
|
K
|
:Konstanta Boltzman, 1.3806 x 10-23
J/K
|
q
|
:Muatan elektron, 1.6021 x 10-19
Coulomb
|
Nilai light-generated current Ipv bergantung pada intensitas matahari G seperti ditunjukkan persamaan II.7,
Gn adalah besar intensitas nominal (1000 W/m2), KI merupakan konstanta arus yang pada umumnya terdapat pada datasheet produk, ΔT adalah temperatur aktual dalam kelvin dikurangi dengan temperatur nominal. Sedangkan nilai light-generated current nominal IPV,n, nilainya sesuai persamaan III.8 dimana Isc,n adalah arus short circuit panel surya. Io adalah arus saturasi, nilai tipikalnya adalah antara 10-6 hingga 10-15 A [31]. Secara matematis Io memiliki persamaan sebagai berikut:
Koefisien arus KI dan koefisien tegangan KV akan mempengaruhi Io yang mana sangat dependen terhadap suhu. Sebagian besar nilai dari parameter yang diperlukan untuk menyelesaikan persamaan III.5 hingga III.9 umumnya dapat ditemukan di dalam datasheet produk panel surya, namun terdapat beberapa parameter yang nilainya tidak diberikan, diantaranya adalah, light-generated current Ipv, resistansi seri Rs dan resistansi paralel Rp, konstanta dioda a, serta arus balik saturasi diode I0. Ipv dapat diselesaikan dengan persamaan III.7 dan III.8, sedangkan arus saturasi dioda Io dapat diselesaikan sesuai persamaan III.9. Untuk konstanta dioda a, variasi nilainya adalah 1 ≤ a ≤ 2. Konstanta dioda mengekspresikan derajat keidealan suatu dioda dan nilainya bergantung pada material dan konstruksi fisik dioda, untuk bahan germanium a=1, sedangkan silikon a=2 ( dalam praktek 1.1 ≤ a ≤ 1.8). Dua parameter yang masih belum diketahui adalah Rs dan Rp. Beberapa penelitian telah menghasilkan suatu metode matematis untuk menemukan nilai tahanan ini, namun metode tersebut tetap saja masih membutuhkan data eksperimen. Untuk menemukan kedua parameter resistansi ini harus dipahami terlebih dahulu bahwa hanya terdapat satu data Rs dan Rp yang memenuhi Pmax,m=Pmax,e=Vmp.Imp pada titik {Vmp,Imp} di dalam kurva I-V, sehingga daya maksimum Pmax,m yang dihitung menurut persamaan 3 akan sama dengan daya maksimum berdasarkan datasheet (Pmax,e). Hubungan antara Rs dan Rp dapat ditemukan apabila dianggap Pmax,m=Pmax,e, sehingga akan dijumpai persamaan sebagai berikut:
Persamaan di atas memiliki makna bahwa untuk setiap nilai Rs akan ada nilai Rp. Tujuan yang ingin dicapai sekarang adalah didapatkannya nilai Rs yang dapat menyebabkan puncak kurva P-V secara matematis sama dengan titik puncak daya secara eksperimen/sesuai datasheet (Vmp,Imp). Untuk mendapatkan nilai ini maka perlu dilakukan proses iterasi hingga Pmax,m memiliki nilai yang sama dengan Pmax,e.
Artikel ini merupakan bagian dari makalah tesis penulis (lihat)
Referensi:
[30]
|
Marcelo G.V. (2009):
Comprehensive Approach to Modelling and Simulation of Photovoltaic Arrays. IEEE Transaction on power Electronics Vol.
24 No. 5, pp 1198-1208.
|
[31]
|
Rashid, M. (2004): Power
Electronics: Circuit, Device, and Application 3hd ed. Pearson Education.
|

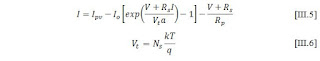


No comments:
Post a Comment